Aritmatika

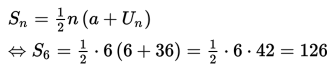
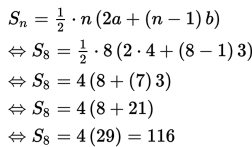
Aritmatika adalah cabang matematika yang berkaitan dengan hitungan. Dalam bahasa arab aritmatika sering dikenal dengan nama ilmu “al hisab”.Adapun ruang lingkup kajiannya adalah melakukan proses perhitungan atas benda benda yang didapati dalam kehidupan sehari hari. Perhitungan tersebut meliputi proses penjumlahan, pengurangan, perkalian serta pembagian.

Untuk kepentingan perrhitungan tersebut para ahli matematika menciptakan satu set simbol bilangan yang merunjuk pada “kuantitas”tertentu. Misalnya, simbol 1 memiliki nilai tertentu, yang tentunya akan berbeda dengan simbol 2, 3 dan seterusnya. Simbol-simbol inilah yang kita sebut dengan “angka”.

Manfaat belajar Aritmatika 

Melalui belajar aritmatika seorang anak akan memperoleh manfaat diantaranya:

1)     Meningkatkan kemampuan berhitung lebih cepat di atas rata-rata anak.

2)      Kemampuan cara berfikir lebih cepat dan tepat.

3)   Membiasakan diri dengan angka-angka, membuat anak tidak lagi alergi pada pelajaran eksakta.

Dalam kehidupan sehari hari sering digunakan untuk:

 kegiatan sehari-hari seperti berdagang, bertransaksi, dan lain -lain. Aritmatika kompleks atau rumit digunakan untuk merancang bangunan dan alat-alat lain.

Dalam kehidupan sehari-hari, terdapat beberapa contoh masalah yang dapat diselesaikan dengan menggunakan konsep barisan dan deret aritmetika. Berikut ini ad tentukanlah 20 suku pertama dari deret aritmatika 4 + 7 + 10 + 13 alah beerapa contohnya.  

Contoh 1

Fikri memiliki seutas tali rafia yang dipotong menjadi 6 bagian dan membentuk barisan aritmetika. Panjang tali yang terpendek adalah 6 cm dan yang terpanjang 36 cm. Tentukan panjang rafia semula.

Penyelesaian:

banyak potongan tali rafia = n = 6 
panjang tali terpedek = a = 6 cm 
panjang tali terpanjang = U6 = 36

Panjang rafia semula adalah jumlah seluruh panjang potongan tali rafia (S6), sehingga

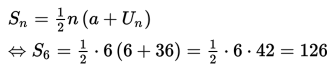
Jadi, panjang tali rafia semula adalah 126 cm.

Contoh 2

Dalam sebuah gedung terdapat 4 buah kursi di barisan terdepan. Banyaknya kursi pada baris-baris berikutnya selalu lebih banyak 3 kursi dibanding baris sebelumnya. Jika terdapat 8 baris kursi, maka tentukan banyaknya kursi dalam gedung tersebut.

Penyelesaian:

Diketahui barisan-barisan kursi yang membentuk barisan aritmetika dengan,
kursi terdepan = a = 4
selisih banyaknya kursi tiap baris = b = 3 
banyak baris kursi = n = 8.

Banyaknya kursi dalam gedung adalah jumlah kursi dari baris terdepan sampai ke-8 (S8), sehingga

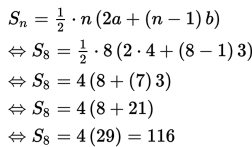
Jadi, banyaknya kursi dalam gedung tersebut adalah 116 buah.

A. Barisan Aritmatika

U1, U2, U3, .... Un disebut barisan aritmatika, dengan U2 - U1 = U3 - U2 = U4 - U3 = ..... Un - Un - 1 = Konstanta. Konstanta ini disebut beda dan dinyatakan dengan b.

Jika suku pertama dinyatakan U1 dinamakan a,  maka diperoleh :

U2 - U1 = b --> U2 = U1 + b = a + b 

U3 - U2 = b --> U3 = U2 + b = ( a + b ) + b = a + 2b 

U4 - U3 = b --> U4 = U3 + b = ( a + 2b ) + b = a + 3b dan seterusnya 

Berikutnya  merupakan  barisan aritmatika : 

a, a + b, a +2b, a + 3b, ...... + ( n - 1 ).b 

Suku ke-n : Un = a  + ( n - 1 ).b 

Contoh :

1. Tentukanlah suku ke-20 dari barisan 5, 7, 9, .... 

Jawab : 

a = 5

b = 7 - 5 = 2

n = 20 

Un = a + ( n - 1 ) b

     = 5 + ( 20 - 1 ).2

     = 43 

Jadi suku ke-20 = 43

2. Sebuah barisan aritmatika mempunyai suku ke-12 adalah 41 dan suku ke-8 adalah 25. Tentukanlah suku pertama, beda, dan suku ke-50

Jawab :

U12 = 41 --> a + 11b = 41 

U8.  = 25 --> a + 7b = 25 

                             4b = 16

                               b = 4

       a + 7.4 = 25

       a = - 3

U50 = a + 49.b

        = -3 + 49.4

        = 193

B. Deret aritmatika 

Apabila suku - suku suatu barisan aritmatika dijumlahkan, maka diperoleh deret aritmatika. Jumlah n suku suatu deret aritmatika. Jika suku terakhir Un, maka suku sebelumnya ( Un - b) , sebelumnya lagi ( Un - 2b) dan seterusnya.  

  Sn = a + ( a + b ) + ( a + 2b ) + ....... + ( Un - 2b ) + ( Un - b ) + Un 

  Sn = Un +  ( Un - b ) + ( Un - 2b ) + ..... + ( a + 2b ) + ( a + b ) + a 

2Sn = ( a + Un)  + ( a + Un ) + ( a + Un ) + ..... + ( a + Un ) + ( a + Un) + ( a + Un ) 

2Sn = n.( a + Un )   

Sn = n/2 ( a + Un )                  

Sn dapat juga dinyatakan sbb. 

Sn = n/2 { 2a + ( n - 1 ).b }

Ket :

a = suku pertama 

b = beda 

n = banyak suku 

Sn = jumlah ke-n suku pertama dari deret aritmatika 

Contoh :

1. Jumlah n suku pertama suatu deret aritmatika ditentukan oleh rumus Sn = 2n² - 6n. Carilah suku ke-20. 

Jawab : 

Sn = 2n² -6n 

Sn-1 = 2 ( n - 1 )² - 6 ( n - 1 ) 

        = 2 ( n² - 2n + 1 ) - 6 ( n - 1 ) 

        = 2n² - 10n + 8 

Un = Sn - Sn-1

     = ( 2n² - 6n)  - ( 2n² - 10n + 8 )

     = 4n - 8 

U20 = 4.20 - 8 = 72 

Jadi, suku ke-20 = 72

2. Tentukanlah 20 suku pertama dari deret aritmatika 4 + 7 + 10 + 13 + ...... 

Jawab : 

a = 4

b = 3 

n = 20

Sn = 20 /2 ( 2a + ( n - 1 ).b 

S20 = 20/2 ( 2.4 + ( 20 - 1 ).3 )

        = 10 ( 8 + 19 ).3 

        = 650